Les fonctions linéaires et affines

Définition d'une fonction
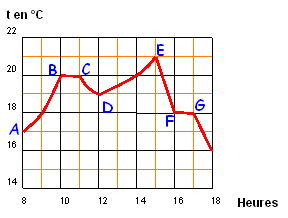
Sens de variation d'une fonction
Maximum et minimum d'une fonction
Fonction linéaire
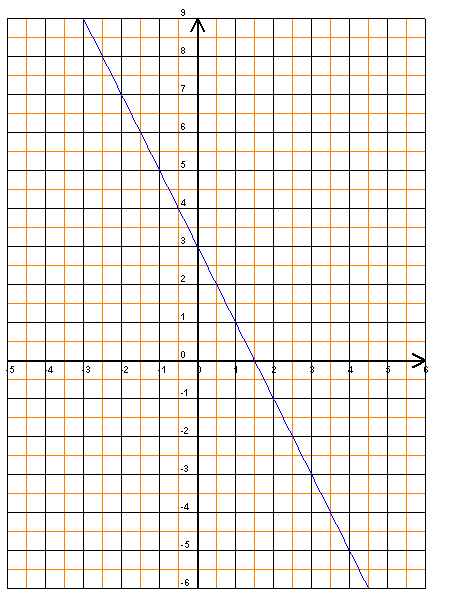
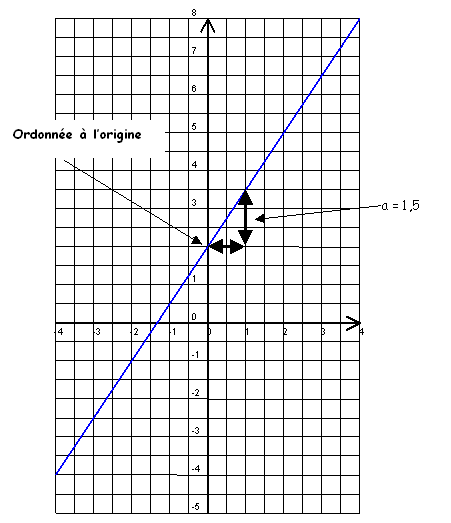
Fonction affine
Recherche d'une équation de droite
Propriétes des droites

Définition d'une fonction

Une fonction numérique est une relation qui a un nombre x fait correspondre au plus un nombre y (Au plus signifie 1 ou 0).
° Notation :  Si la fonction est notée f, on écrit : f : x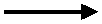  y
                                                                        x est la variable
                                                                        y est l'image de x par la fonction f
                                                                        On note y = f(x)

Sens de variation d'une fonction

Un enregistreur de température, placé dans une salle de classe, a donné l'enregistrement ci-dessous de 8 heures à 18 heures.
Cette courbe est la représentation graphique de la fonction f qui, à chaque instant x, associe sa température f(x).
Elle est définie sur l'intervalle [8 ; 18].


        --> Entre 8 h et 10 h, la température:

   augmente        diminue        reste constante
    On dit que la fonction f est croissante sur l'intervalle [8 ; 10].
    La fonction f est aussi croissante sur l'intervalle [ ; ]
     
    --> Entre 10 h et 11 h, la température:

   augmente        diminue        reste constante
       On dit que la fonstion f reste constante sur l'intervalle [10 ; 11].

    La fonction f est aussi constante sur l'intervalle [ ; ]
    --> Entre 11 h et 12 h, la température:

   augmente        diminue        reste constante
On dit que la fonction f est décroissante sur l'intervalle [11 ; 12] .
    La fonction f est aussi décroissante sur les intervalles [ ; ] et [ ; ]. (Remplir les intervalles dans l'ordre.)

********** **********

  
Donner le sens de variation  d'une fonction sur un intervalle, c'est dire si la fonction est croissante, décroissante ou constante sur cet intervalle.

Maximum et minimum d'une fonction
    --> Entre 8 h et 12 h, la température la plus élevée est : °C.
On dit que sur l'intervalle [8 ; 12], 20 est le maximum de la fonction f.
Le maximum de f sur [14 ; 16] est : °C ; le maximum de f sur [8 ; 18] est : °C.
    --> Entre 11 h et 13 h, la température la plus basse est : °C.
On dit que sur l'intervalle [11 ; 13], 19 est le minimum de la fonction f.
Le minimum de f sur [12 ; 16] est : °C ; le minimum de f sur [8 ; 18] est : °C .     

********************
Soit f une fonction définie sur l'intervalle [a ; b]. La fonction f admet un minimum m sur [a ; b] lorsque m est la plus petite valeur  de f(x).
Soit f une fonction définie sur l'intervalle [a ; b]. La fonction f admet un maximum M sur [a ; b] lorsque M est la plus grande valeur  de f(x).


Fonction linéaire

Exemple de fonction linéaire :
On considère deux suites de nombres proportionnels.
Par exemple : 
x -3 0 1 2 5 x
y -7,5 0 2,5 5 12,5
Si on appelle x les nombres de la première ligne et y ceux de la deuxième ligne, compléter le tableau précédent en trouvant le nombre qui donne la deuxième ligne à partir de la première.
********************
On dit que l'on passe de x à y en effectuant: y = 2,5x par la fonction linéaire dont le coefficient est 2,5.

Cette fonction linéaire se note : x --> 2,5x .

Si on désigne cette fonction linéaire par la lettre f, on écrit: f(-3) = -7,5 f(0) = 0 etc...        f(-3) se prononce f de -3.

 On dit  que -7,5 est l'image de -3 et, de façon plus générale, que 2,5x est l'image de x.

Représentation graphique d'une fonction linéaire :
On représente les x sur l'axe des abscisses et les images y sur l'axe des ordonnées.

° Propriété:
La représentation graphique d'une fonction linéaire est une droite passant par l'origine.

° Vocabulaire :
On dit que cette droite a pour équation y = 2,5x.
On dit aussi que son coefficient directeur est 2,5.



Fonction affine

Définition et exemple :
Étant donné deux nombres fixés a et b, la fonction x --> ax + b est appelée fonction affine.
Compléter le tableau suivant :

-2x + 3 x 1 0 4 -1 -2 3
y

********************

Si on appelle f cette fonction affine, on peut écrire : f(1) = 1, f(0) = 3 etc...

Représentation graphique d'une fonction affine :
A partir du tableau de valeurs précédent, on place les points de coordonnées ( x ; y ) dans un repère et on trace la ligne reliant tous ces points.

° La représentation graphique d'une fonction affine est une droite.

° Vocabulaire :   Cette droite a pour équation y = -2x + 3
                        Son coefficient directeur est -2

Recherche d'une équation de droite

I) On connait le coefficient directeur et un point de la droite :
Exemple : Recherchons l’équation de la droite passant par A(5 ; 2) et de coefficient directeur a = - 0,25.
L’équation générale de la droite est `y` = a`x` + b
On peut donc écrire, si on remplace a par sa valeur : `y` =  `x` + b
Puisque la droite passe par le point A, remplaçons `x` par 5 et `y` par 2
= - 0,25 x  + b
 = + b
+ = b

********************

b = 3,25
La droite a pour équation y = - 0,25x + 3,25
II) On connait deux points de la droite : 

Exemple : Dans un repère orthonormé d’unité 1 cm , placer les points A(-2 ; -1) et B(2 ; 5)
Tracer la droite passant par A et B, donner une équation de cette droite.

° Résolution par le calcul :  On fait correspondre les x1 , y1 , x2 et y2onnées de A et de B aux lettres x1 , y1 , x2 et y2 .
On obtient le coefficient directeur a en effectuant le calcul :
` a = (y_2 - y_1)/(x_2 - x_1)`

On remplace x1 , y1 , x2 et y2 par leurs valeurs, on obtient : `a = (5 - -1)/(2 - -2) = (5 + 1)/(2 + 2) = 6/4 = 3/2 = 1,5`

L’équation de la droite devient  y = 1,5x + b et passe par le point A (on aurait pu choisir le point B).
-1 = 1,5 x (-2) + b
-1 = -3 + b
b = 2
L’équation est donc y = 1,5x + 2
° Résolution graphique :  On mesure sur le graphique l’évolution de y lorsque x augmente de 1. Cette évolution correspond au coefficient directeur a.    b se lit en prenant l’ordonnée à l’origine.

Dans l'exemple précédent, lorsque x augmente de 1, y augmente de 1, 5 donc a = 1,5
L’ordonnée à l’origine est 2 donc b = 2
La droite a pour équation y = 1,5x + 2.

Propriétés des droites

I) Droites parallèles :

Deux droites qui ont un même coefficient directeur sont parallèles.
Exemple : D1 : y = 2x + 1 et D2 : y = 2x – 1      D1 // D2 car elle ont toutes les deux le même coefficient directeur a = 2.

II) Droite perpendiculaires :

Dans un repère orthonormal, deux droites dont le produit des coefficients directeurs est égal à –1 sont perpendiculaires.
Exemple : Dans un repère orthonormal, les droites D1 : y = 4x - 2 et D2 : y = - 0,25x sont perpendiculaires car (4) x (-0,25) = - 1.