Aide sur les fonctions linéaires et affines

Fonctions linéaires :
 
Étant donné un nombre a, une fonction f qui à tout nombre x fait correspondre le nombre f(x) = ax est une fonction linéaire.
Le nombre a est appelé coefficient de la fonction linéaire.
Exemple : f(2) = 4, on obtient a en effectuant le rapport a = `4/2` .
° f est croissante si a est positif, décroissante  si a est négatif.
° À toute situation de proportionnalité, on peut associer une fonction linéaire.

La représentation graphique d'une fonction linéaire de coefficient a est la droite qui passe par l'origine du repère et par le point de coordonnées (1 ; a).
La droite représentative de cette fonction a pour équation y = ax.   a est appelé le coefficient directeur de la droite.


Fonctions affines :

Étant donné deux nombres a et b, une fonction f qui a tout nombre x fait correspondre le nombre f(x) = ax + b est une fonction affine.
 ° f est croissante si a est positif, décroissante  si a est négatif.
° Si b = 0, f est une fonction linéaire.
° Si a = 0, f est une fonction constante.

La représentation graphique de la fonction affine f définie par f(x) = ax + b est une droite qui passe par le point de coordonnées (0 ; b).
La droite représentative de la fonction f a pour équation y = ax + b. Le nombre a est le coefficient directeur de la droite, le nombre b est son ordonnée à l'origine.

Équation d'une droite :

Trouver l'équation d'une droite passant par deux points A(x1 ; y1) et B(x2 ; y2).
Résolution par le calcul :

Toute droite a pour écriture générale y = ax + b.
On obtient le coefficient directeur a par le calcul : a = `(y_2 - y_1)/(x_2 - x_1)`
Exemple : Trouver l'équation de la droite passant par A(-2 ; -1) et B(2 ; 5). On remplace les lettres par leurs valeurs
a = `(5 - -1)/(2 - -2) = (5 + 1)/(2 + 2) = 6/4 = 3/2 = 1,5`.

L'équation de droite est donc `y = 1,5x + b`. Pour trouver b, on sait que cette droite passe par A ou B.

Remplaçons les coordonnées x et y par les valeurs de B par exemple.
5 = 1,5 x 2 + b
5 = 3 + b
5 - 3 = b
L'équation est donc y = 1,5x + 2.
Résolution graphique :  On mesure sur le graphique l’évolution de y lorsque x augmente de 1. Cette évolution correspond au coefficient directeur a.    b se lit en prenant l’ordonnée à l’origine.

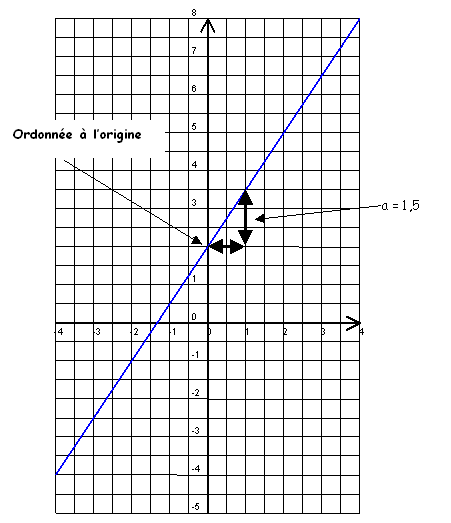
Lorsque x augmente de 1, y augmente de 1, 5 donc a = 1,5
L’ordonnée à l’origine est 2 donc b = 2
La droite a pour équation y = 1,5x + 2.


Droites parallèles, droites perpendiculaires :


Deux droites sont parallèles si leurs coefficients directeurs sont égaux.
Exemple: Soient les droites `Delta` : y = -3x + 2   et `Delta'` : y = -3x - 4 .
`Delta //// Delta'` car leurs coefficients directeurs sont égaux.

Deux droites sont perpendiculaires si le produit de leurs coefficients directeurs est égal à -1.
Exemple: Soient les droites `Delta` : y = -2x + 2   et `Delta'` : y = 0,5x - 4 .
`Delta _|_ Delta'` car -2 x 0,5 = -1.