CH IV Statistique .

Auteur: Daniel GENELLE                              (Optimisé pour Mozilla Firefox.)  

Pour pouvoir lire les mots de vocabulaire cachés (fond jaune), il suffit de passer la souris sur le mot.

I) Rappels de seconde.
1) Le caractère d'une série statistique.
2) La fréquence.
3) Les représentations graphiques.
II) Les indicateurs de tendance centrale.
1) Le mode, la calsse modale.
2) La moyenne.
3) La médiane d'une série statistique.
III) Les indicateurs de dispersion: étendue, écart type, quartiles, écarts interquartile.
1) L'étendue.
2) Evaluer la dispersion d'une série avec l'écart type.
3) Evaluer la dispersion d'une série avec l'écart interquartile.
IV) La courbe de Gauss et la boite à moustaches.
1) La courbe de Gauss.
2) la boite à moustaches.
V) Problèmes.
VI) Quelques fonctions d'OpenOffice utilisables en statistique.

I) Rappels de seconde.

1) Le caractère d'une série statistique.

☺ Le caractère d’une série statistique peut être qualitatif ou quantitatif. Lorsqu’il est quantitatif, il sera ou discret ou continu.

Caractère qualitatif Caractère quantitatif discret continu

Compléter les phrases. Il faut sélectionner les expressions.              

Ex1 : L’étude porte sur le nombre de voitures rouges, vertes, bleues et noires qui se trouvent sur un parking.
Le caractère étudié sera ici .

Ex2 : L’étude porte sur le nombre de frères et sœurs qu’un élève de lycée peut avoir. Un élève pourra avoir 0 ; 1 ; 2 ; 3 ; 4 … frères et sœurs.
Le caractère étudié sera ici .

Ex3 : L’étude porte sur l’âge des élèves qui passent le bac. On pourra classer le nombre d’élèves dans des intervalles : [16 ; 17[ ; [17 ; 18[ ; [18 ; 19[ …
Le caractère étudié ici sera ici .

2) La fréquence.

☺   La fréquence fi d’une valeur ou d’une classe de valeurs d’un caractère est le rapport    ni 
━		 où ni est l’effectif et N l’effectif total.
 N 
  fi =    ni 
━
 N 

3) Les représentations graphiques.

Exemple 1 : La répartition selon la surface en m2, des 67 magasins d’un centre commercial est représenté par le diagramme en bâtons suivant.
a) Quel est la nature de ce caractère ?
b) A l’aide du graphique, compléter le tableau :              

a) La nature du caractère est .
b) A l'aide du graphique, compléter le tableau.
exemple1.jpg
Surface d’un magasin (en m2)
xi		 Total
Nombre de magasins
ni
Fréquence fi
(arrondie à 0,001)

Exemple 2 : On relève dans une station service, une semaine donnée, le volume d’essence, acheté par 895 clients. Les résultats sont représentés par l’histogramme suivant :
a) Quelle est la nature de ce caractère ?
b) A l’aide du graphique, compléter le tableau :              

a) La nature du caractère est .
b) A l'aide du graphique, compléter le tableau.
exemple2.jpg
Volume d'essence (en L) Nombre de clients Fréquence fi
(en % arrondi au centième)
[  [
[  [
[  [
[  [
[  [
[  [
[  [
[  [
Total

II) Les indicateurs de tendance centrale.

1) Le mode, la classe modale.

☺ Le mode est la valeur du caractère ayant le plus grand effectif. Une distribution avec un seul mode est dite unimodale, avec deux modes, elle est dite bimodale.
Dans le cas de répartition en classes d’égales amplitudes, la classe modale désigne celle qui a le plus grand effectif. Le mode est le centre de cette classe.

Exemple: On dispose de deux séries de distances entre le domicile et le lycée (en km) rangées en classes. Compléter.
Ecrire les classes modales et les modes dans l'ordre d'apparition.              

exemple3.jpg La classe modale est: [  [.

Le mode est .
exemple4.jpg Les classes modales sont: [  [ et [  [ .

Les modes sont et .

2) La moyenne.

On a relevé les âges des participants à une manifestation sportive :

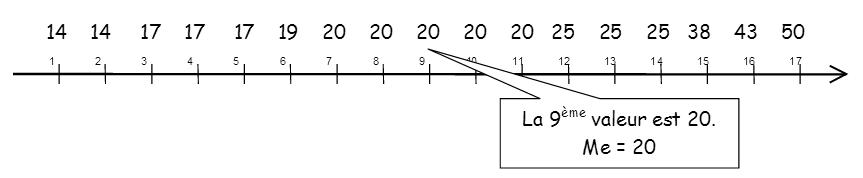
Âges xi 14 17 19 20 25 38 43 50
Effectifs ni 2 3 1 5 3 1 1 1

La moyenne x  de cette série est obtenue en divisant la somme des valeurs ni . xi par l’effectif total N.

Calculer la moyenne de cette série statistique. Donner le résultat au centième près.              

x  =  
━━━		  = 

Lorsque les valeurs sont regroupées en classes, la somme des valeurs est obtenue en multipliant chaque valeur centrale par l’effectif de la classe.

On peut obtenir la moyenne directement à l’aide de la calculatrice : Voir 2nd CH IV Statistique II Utilisation de la calculatrice.

On peut également utiliser un tableur pour obtenir cette moyenne. Voir 2nd Fiche Calcul des paramètres statistiques à l’aide du tableur.

L’interprétation de la moyenne est la suivante : L’âge moyen des participants à cette manifestation est de 23,76 ans.

3) La médiane.

La médiane Me de la série est un nombre qui découpe la liste des âges, rangée dans l’ordre croissant, en deux listes. Si l’effectif total est impair, on obtient la médiane en prenant la valeur correspondant à l’effectif + 1 divisé par 2.
La médiane correspond ici à la     17 + 1
━━━		    = 9ième valeur.
2

On place les âges des 17 participants à la manifestation sportive dans l’ordre croissant :

mediane1.jpg

Lorsque l’effectif est pair, la médiane sera la moyenne des deux valeurs correspondantes aux rangs
 effectif
━━━		   et    effectif
━━━		  + 1.
2 2

On peut obtenir la médiane directement à l’aide de la calculatrice : Voir 2 nd CH IV Statistique II Utilisation de la calculatrice.

On peut également utiliser un tableur pour obtenir cette médiane: Voir 2 nd Fiche Calcul des paramètres statistiques à l’aide du tableur.

L’interprétation de la médiane est la suivante : « La moitié des participants a 20 ans et moins de 20 ans et l’autre moitié a 20 ans et plus de 20 ans. »

Exercice N°1: Pour chaque série statistique :
1) Déterminer le ou les modes :
2) Déterminer, avec une calculatrice, la moyenne et la médiane.
Les résultats ne seront pas arrondis....              

Valeurs xi 2 8 10 14 21 25 30
Effectifs ni 3 5 7 10 8 4 3

Le mode = , la moyenne = et la médiane = .

Valeurs xi 10 15 30 40 45 50 55 65
Effectifs ni 1 1 2 4 3 2 1 1

Le mode = , la moyenne = et la médiane = .

Exercice N°2: Dans une classe de première, on demande aux élèves le nombre d’activités sportives qu’ils pratiquent régulièrement. On obtient les réponses suivantes : 2 élèves ne font aucun sport ; 10 élèves pratiquent un sport ; 8 élèves pratiquent deux sports ; 6 élèves pratiquent trois sports ; 4 élèves pratiquent quatre sports.
a) Déterminer la population et le caractère étudié. Quelle est la nature de ce caractère ?
b) Regrouper ces résultats dans un tableau.
c) Quel est le nombre d’activités sportives le plus fréquent dans cette classe.
d) Déterminer avec une calculatrice la moyenne de cette série statistique. Interpréter le résultat par une phrase.
e) Déterminer avec une calculatrice la médiane de cette série statistique. Interpréter le résultat par une phrase.
             

a) La population correspond au , la caractère étudié correspond au , la nature de ce caratère est .

b) Regrouper ces résultats dans un tableau.

Nombre de sports xi Nombre d'élèves ni


c) Le nombre d’activités sportives le plus fréquent dans cette classe est activités.
L’indicateur de tendance central associé est
d) La moyenne = . En moyenne, les élèves pratiquent activités sportives.
e) La médiane = . La moitié des élèves pratique activités sportives et moins.

III) Les indicateurs de dispersion : Étendue, écart type, quartiles, écart interquartile :

1) L’étendue.

☺ L’étendue est la différence entre la plus grande et la plus petite valeur du caractère.

2) Évaluer la dispersion d’une série avec l’écart type :

☺ L’écart type σ indique la dispersion des valeurs de la série autour de leur moyenne.
- Sur la calculatrice Casio, l’écart type correspond à la valeur xσn ou σx.
- Sur la calculatrice TI, l’écart type correspond à la valeur σx.

Voici le relevé de 3 notes de mathématiques de Théa, Hector et Basile.
Calculer à l’aide de la calculatrice pour chaque élève la moyenne x  et l’écart type σ.
On arrondira au centième si nécessaire.              

Théa   11     9     10   x  = σ =
Hector   7     15     8   x  = σ =
Basile   11     3   16 x  = σ =

Dans ce cas les moyennes sont les mêmes, les écarts types indiquent une plus grande régularité des notes pour Théa que pour Basile.
☺ Le couple (moyenne ; écart type) rend compte d’un certain point de vue de la série.

3) Évaluer la dispersion d’une série avec l’écart interquartile :

☺ Le premier quartile Q1 partage les valeurs du caractère, rangées en ordre croissant, en deux groupes : le 1er groupe représente à peu prés 25 % de l’effectif total et le 2ème groupe à peu près 75 %.
☺ Le troisième quartile Q3 partage les valeurs du caractère, rangées en ordre croissant, en deux groupes : le 1er groupe représente à peu prés 75 % de l’effectif total et le 2ème groupe à peu près 25 %.
☺ L’écart interquartile Q3 – Q1 représente 50 % de l’effectif total.
☺ Le couple (médiane ; écart interquartile) rend compte d’un certain point de vue de la série.

La répartition des années d’ancienneté de 24 employés d’une entreprise est donnée par le tableau suivant :
1) Déterminer l’étendue de cette série. Interpréter ce résultat.
2) Déterminer, à l’aide de la calculatrice, la moyenne et l’écart type On arrondira au dixième.
3) Déterminer, à l’aide de la calculatrice, le premier et le troisième quartile. Interpréter ces résultats.
4) Calculer l’écart interquartile Q3 – Q1. Interpréter ce résultat.              

Années d’ancienneté xi   1     2     3     4     5  
Nombre d’employés ni   5     5     7     4     3  
1) Déterminer l’étendue de cette série. Interpréter ce résultat.
L'étendue = - = .
ans séparent les employés dont l’ancienneté est la plus petite de ceux dont l’ancienneté est la plus grande.

2) Déterminer, à l’aide de la calculatrice, la moyenne et l’écart type arrondis à 0,1.
x  et σ = .

3) Déterminer, à l’aide de la calculatrice, le premier et le troisième quartile. Interpréter ces résultats.
Q1 = .
des employés ont et des employés ont .
Q3 = .
des employés ont et des employés ont .

4) Calculer l’écart interquartile Q3 – Q1. Interpréter ce résultat.
Q3 – Q1 = - = .
des employés ont entre et ans d'ancienneté.

IV) La courbe de Gauss et la boite à moustaches :

1) La courbe de Gauss :

Un laboratoire d’analyse biologiques étudie les taux de calcium (en mg/L) de 220 personnes. Les résultats sont représentés par un histogramme, sur lequel la courbe tracée visualise l’allure de la série. Cette courbe, en forme de cloche, est appelée courbe de Gauss.
☺ Pour une série statistique dont la représentation graphique a l’allure de la courbe de Gauss, les valeurs sont réparties à peu prés symétriquement autour de leur moyenne. Environ 95 % d’entre elles appartiennent à l’intervalle [x  - 2σ ; x  + 2σ].
gauss.jpg

Calculer, à l’aide de la calculatrice, les moyenne (arrondie à l'unité) et écart type (arrondi au dixième) de la série précédente.
Calculer x  - 2σ puis x  + 2σ.
Calculer le nombre de personnes dont le taux, en mg/L, est compris entre 84 et 102.
Exprimer ce nombre en pourcentage par rapport au nombre total de personnes (arrondi à l'unité). Cela vous semble-t-il cohérent par rapport à l’affirmation de l’encadré précédent.              

Calculer, à l’aide de la calculatrice, les moyenne (arrondie à l'unité) et écart type (arrondi au dixième) de la série précédente.
x  = σ =

Calculer x  - 2σ puis x  + 2σ.
x  - 2σ = et x  + 2σ =

Calculer le nombre de personnes dont le taux, en mg/L, est compris entre 84 et 102.
Nombre = + + + + + + + + = .

Exprimer ce nombre en pourcentage par rapport au nombre total de personnes (arrondi à l'unité). Cela vous semble-t-il cohérent par rapport à l’affirmation de l’encadré précédent.
Pourcentage = %.
Ce pourcentage cohérent par rapport à l’affirmation de l’encadré précédent.

2) La boîte à moustaches :

☺ On représente sur un graphique que l’on appelle « boîte à moustaches » un certain nombre d’indicateurs statistiques. Chaque « boîte » est délimitée par les premiers et troisièmes quartiles, et les « moustaches » par les valeurs minimales et maximales de la série associée. La médiane est marquée par le segment vertical à l’intérieur de la boîte.

Min Q 1 Me Q 3 Max

Exercice 1a: Compléter le tableau en y reportant la valeur des indicateurs statistiques donnés par le diagramme en boîte à moustaches.              

exercicea.jpg

Minimum Premier quartile Médiane Troisième quartile Maximum

Exercice 1b: Compléter le tableau en y reportant la valeur des indicateurs statistiques donnés par le diagramme en boîte à moustaches.              

exerciceb.jpg

Minimum Premier quartile Médiane Troisième quartile Maximum

Exercice 1c: Compléter le tableau en y reportant la valeur des indicateurs statistiques donnés par le diagramme en boîte à moustaches.              

exercicec.jpg

Minimum Premier quartile Médiane Troisième quartile Maximum

Exercice 1d: Compléter le tableau en y reportant la valeur des indicateurs statistiques donnés par le diagramme en boîte à moustaches.              

exerciced.jpg

Minimum Premier quartile Médiane Troisième quartile Maximum

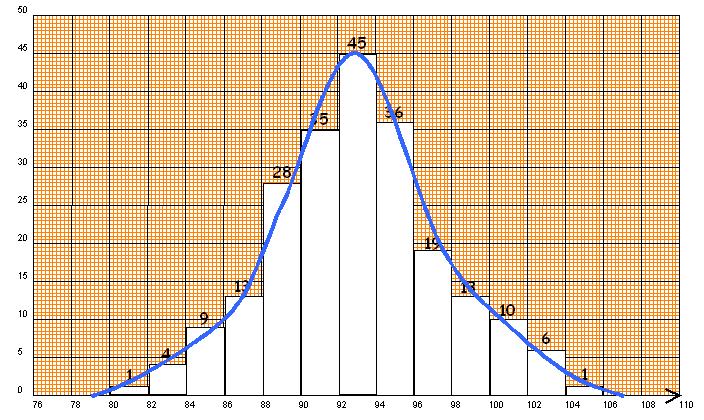
Exercice 2: La glycémie à jeun est un test sanguin effectué lorsque le patient a passé 12 heures sans s’alimenter ni boire (sauf de l’eau). Pour une personne non diabétique, le taux normal de glycémie est compris entre 0,70 mg/L et 1,10 mg/L. Un laboratoire a réalisé des analyses de glycémie à jeun sur 50 personnes.
Les résultats sont regroupés dans le tableau suivant :
a) Quel est le taux de glycémie le plus fréquent de ces personnes ?
b) Quel est l’écart maximal des taux de glycémie de ces personnes ?
c) Quelle est la glycémie moyenne de ces personnes ?(Arrondir au millième)
d) Quel le taux médian de glycémie de ces personnes ?
e) Quel est le pourcentage de personnes dont le taux de glycémie est normal ?
             

Glycémié xi en mg/L Nombre de personnes ni
  0,65     1  
  0,68     1  
  0,74     3  
  0,81     5  
  0,83     10  
  0,87     11  
  0,92     8  
  0,96     6  
  1,00     1  
  1,02     1  
  1,11     2  
  1,13     1  

a) Le taux de glycémie le plus fréquent est mg/L.

b) L’écart maximal est – = .

c) Moyenne (arrondie au millième) = mg/L.

d) Me = mg/ L.

e) Pourcentage = %.

V) Problèmes.

Problème N°1: Afin de proposer un service de bus, une enquête a été réalisée sur la durée du trajet, en minutes, des 400 employés de l’entreprise « Fabric » pour se rendre sur leur lieu de travail. Ce service sera mis en place si la durée moyenne du trajet est supérieure à 20 minutes.
a) Compléter le tableau statistique suivant :
b) Quelle est la classe modale ?
c) Déterminer le pourcentage d’employés dont la durée du trajet est supérieure ou égale à 20 min.
d) Déterminer, à l’aide d’une calculatrice, la moyenne de cette série statistique.
e) Indiquer si le service de bus sera mis en place par l’entreprise. Justifier la réponse.
             

Durée du trajet
en min.		 Centre de classe
xi		 Nombre d'employés
ni		 Fréquence fi
(en %)
[ 0 ; 10 [ 40
[ 10 ; 20 [ 80
[ 20 ; 30 [ 90
[ 30 ; 40 [ 120
[ 40 ; 50 [ 50
[ 50 ; 60 [ 20

b) La classe modale est [ ; [.

c) Le pourcentage d’employés dont la durée du trajet est supérieure ou égale à 20 min est %.

d) La moyenne de cette série statistique est x  = min.

e) Le service de bus mis en place car la durée moyenne du trajet est à 20 min.


Problème N°2: La vente du bois de chauffage ne peut pas se faire au « poids » car la masse varie de manière importante suivant les essences et le taux d’humidité du bois. On mesure le taux d’humidité en pourcentage des bûches livrées à l’aide d’un appareil. Les mesures sont rassemblées dans le tableau.
a) Compléter le tableau statistique :
b) Déterminer l’indication moyenne (arrondie au dixième) de l’appareil ainsi que son écart type (arrondi au centième).
c) On estime que le bois est prêt à l’emploi si l’indication moyenne de l’appareil est inférieure à 20 et l’écart type inférieur à 3. Indiquer si le bois livré est prêt à l’emploi.
             

a) Compléter le tableau statistique :
Indications de l'appareil Centres de classes Nombre de bûches testées
  [10 ; 14[     410  
  [14 ; 18[     820  
  [18 ; 22[     1100  
  [22 ; 26[     670  

b) Déterminer l’indication moyenne (arrondie au dixième) de l’appareil ainsi que son écart type (arrondi au centième).           x  = % et σ = %.

c) On estime que le bois est prêt à l’emploi si l’indication moyenne de l’appareil est inférieure à 20 et l’écart type inférieur à 3. Indiquer si le bois livré est prêt à l’emploi.

Le bois livré prêt à l’emploi car est à 3.


Problème N°3: Une machine produit des pièces usinées pour des accessoires de couture. On prélève un échantillon aléatoire de 120 pièces et on mesure leur rayon. Les mesures sont rassemblées dans le tableau.
a) Déterminer le mode et l’étendue de cette série. Interpréter les résultats obtenus.
b) Déterminer, à l’aide d’une calculatrice, le rayon moyen m de cette série de pièces et l’écart type . (arrondir à l’unité).
c) Le rayon annoncé par l’entreprise est 319 mm : celui-ci correspond au rayon x  programmé par l’entreprise sur ses machines-outils. Une étude statistique sur les performances des machines-outils achetées par cette entreprise a montré que, pour une dimension programmée x , les dimensions effectivement obtenues ont graphiquement la forme d’une courbe de Gauss de moyenne x  et d’écart type σ = 1 mm.
Calculer x  - 2σ et x  + 2σ.
d) Calculer, parmi les valeurs observées du tableau, le pourcentage de celles qui appartiennent à l’intervalle [ x  - 2σ ; x  + 2σ ] (arrondir au centième).
e) On rejette les pièces dont le rayon se situe en dehors de l’intervalle [ x  - 2σ ; x  + 2σ ]. Déterminer le nombre, puis le pourcentage de pièces rejetées dans le lot considéré (arrondir au centième).              

Rayon xi (en mm) Nombre de pièces ni
  316     2  
  317     10  
  318     30  
  319     50  
  320     22  
  321     6  

a) Déterminer le mode et l’étendue de cette série. Interpréter les résultats obtenus. Le mode = et l'étendue = - = .

Le nombre de pièces a un rayon de mm.

Le rayon des pièces varie de mm entre et .

b) Déterminer, à l’aide d’une calculatrice, le rayon moyen m de cette série de pièces et l’écart type . (arrondir à l’unité).
Le rayon moyen m = mm et l'écart type est de mm.

c) Le rayon annoncé par l’entreprise est 319 mm : celui-ci correspond au rayon x  programmé par l’entreprise sur ses machines-outils. Une étude statistique sur les performances des machines-outils achetées par cette entreprise a montré que, pour une dimension programmée x , les dimensions effectivement obtenues ont graphiquement la forme d’une courbe de Gauss de moyenne x  et d’écart type σ = 1 mm.
Calculer x  - 2σ et x  + 2σ.
x  - 2σ = et x  + 2σ = .

d) Calculer, parmi les valeurs observées du tableau, le pourcentage de celles qui appartiennent à l’intervalle [ x  - 2σ ; x  + 2σ ] (arrondir au centième).
Le pourcentage = %.

e) On rejette les pièces dont le rayon se situe en dehors de l’intervalle [ x  - 2σ ; x  + 2σ ]. Déterminer le nombre, puis le pourcentage de pièces rejetées dans le lot considéré (arrondir au centième).
Le nombre de pièces rejetté est , ce qui correspond à un pourcentage de %.


VI) Quelques fonctions d’OpenOffice utilisables en Statistique .

On suppose une série de valeurs contenues dans le tableau (A1;H3). Cette série correspond aux relevés des prix du pain (en €) dans 24 boulangeries.

tableur.jpg


☺ Organisation des données.
  =SOMME(A1;H13)     21,90 €     Somme des valeurs  
  =SI(A1=1,1;1;0)   1   1 si la cellule A1 contient 1,1 et 0 dans le cas contraire.  
  =NB.SI(A1:H3;0,9)   8   Nombre de cellule où 0,9 apparaît.  
  =NB.SI(A1:H3;">0,9")   9   Nombre de cellules où la valeur est supérieure à 0,9.
Attention >0,9 est mis entre guillemets " " sans espace.  
  = NB.SI(A1:H3;"<1,1")-NB.SI(A1:H3;">0,9")   14   Nombre de cellules où la valeur est supérieure à 0,9.
Attention >0,9 est mis entre guillemets " " sans espace.  
☺ Calculer des indicateurs de tendance centrale.
  =MODE(A1:H3)     0,9     Mode Mo  
  =MOYENNE(A1:H3)   0,91 €   Moyenne x   
  =MEDIANE(A1:H3)   0,9   Médiane Me  
☺ Calculer des indicateurs de dispersion.
  =MIN(A1:H3)     0,70 €     Valeur minimale xmin  
  =MAX(A1:H3)   1,20 €   Valeur maximale xmax  
  =MAX(A1:H3)-MIN(A1:H3)   0,50 €   Étendue e  
  =QUARTILE(A1:H3;1)     0,8     Premier quartile Q1  
  =QUARTILE(A1:H3;2)     0,9     Deuxième quartile Q2
correspond à la médiane.  
  =QUARTILE(A1:H3;3)     1     Troisième quartile Q3  
  =ECARTYPEP(A1:H3)     0,12     Écart type σ. Attention il faut écrire écart type
avec un P au bout ECARTYPEP.